《熱狂のイフリート/Frenetic Efreet》のエラッタが解除されたことにより、能力の解決時に《イフリート》が場にいなくてもコインが投げられるようになった。これにより、理論上無限にコインを投げることができ、《偶然の出合い/Chance Encounter》とのコンボがレガシーで復活する兆しが見えている(トーナメントレベルかどうかはさておき)。
ところで、このコンボには難点がある。コイントスに負けて《イフリート》が一度死んでしまうと、もうそれ以上コインを投げることができなくなるのである。つまり、能力をスタックに積む数、すなわちコインを投げる回数を初めに宣言しなければならないのだ。
何の気の迷いか《イフリート》と《偶然の出合い》をデッキに入れてトーナメントに臨んでしまった貴方。しかも幸か不幸か2枚とも揃って引いてきた上に、どちらもカウンターされずに場に出てしまった。さあ、あとは何回コインを投げるのか決めるだけだが、回数を少なくして10回勝てなかったら笑えない。20回?30回?・・・それとも、1億回なんて気の遠くなるような回数にしないといけないのだろうか?
簡単のために、「《イフリート》のコイントスをn回行って、《偶然の出合い》に運勢カウンターが10個以上乗る」ことを「コインをn回投げたとき、少なくとも10回は表が出る」ことに置き換えて考えてみよう。これは、高校数学の知識で解ける問題で、余事象を用いると良い。コインをn回投げて、
1度も表が出ない確率はnC0*{(1/2)^0}*{(1/2)^n}
1回だけ表が出る確率はnC1*{(1/2)^1}*{(1/2)^(n-1)}
2回だけ表が出る確率はnC2*{(1/2)^2}*{(1/2)^(n-2)}
・・・
9回だけ表が出る確率はnC9*{(1/2)^9}*{(1/2)^(n-9)}
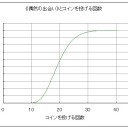
となり、これらの確率を総和した確率は、コインをn回投げて、表が0~9回出る確率だ。余事象の考え方より、1からこの確率を引けば、表が10~n回出る確率が求められる。この計算を人の手で行うのは骨が折れるので、Excelに計算させた。その結果をグラフに示す。
グラフより、25回も投げれば約90%の確率で《偶然の出合い》に運勢カウンターが10個以上乗り、アップキープを待つばかりとなる。さらに、30回を超えると、コイントスを増やすことによる勝利条件達成への寄与がほとんど無くなる。つまり、30回投げようが40回投げようが1億回投げようが、ほぼ100%の確率で《偶然の出合い》に必要なだけの運勢カウンターを乗せることができる (そしてほぼ100%の確率で、その時《イフリート》はこの世にはいない)。
逆に、ひりつくようなギャンブルのスリルを楽しみたいときは、20回程度のコイントスがお勧めだ。6~7割の勝率があるが、残りの3~4割は馬鹿にできない確率である。コンボを揃えておいて自分から不利な状況に突っ込むのはどうかと思うが、自分に課すハードルの高さを自由自在に調節することができるという点で、このコンボの可能性は無限大だ。
# 遠距離レス。お暇な方は検算してみてください。
ところで、このコンボには難点がある。コイントスに負けて《イフリート》が一度死んでしまうと、もうそれ以上コインを投げることができなくなるのである。つまり、能力をスタックに積む数、すなわちコインを投げる回数を初めに宣言しなければならないのだ。
何の気の迷いか《イフリート》と《偶然の出合い》をデッキに入れてトーナメントに臨んでしまった貴方。しかも幸か不幸か2枚とも揃って引いてきた上に、どちらもカウンターされずに場に出てしまった。さあ、あとは何回コインを投げるのか決めるだけだが、回数を少なくして10回勝てなかったら笑えない。20回?30回?・・・それとも、1億回なんて気の遠くなるような回数にしないといけないのだろうか?
簡単のために、「《イフリート》のコイントスをn回行って、《偶然の出合い》に運勢カウンターが10個以上乗る」ことを「コインをn回投げたとき、少なくとも10回は表が出る」ことに置き換えて考えてみよう。これは、高校数学の知識で解ける問題で、余事象を用いると良い。コインをn回投げて、
1度も表が出ない確率はnC0*{(1/2)^0}*{(1/2)^n}
1回だけ表が出る確率はnC1*{(1/2)^1}*{(1/2)^(n-1)}
2回だけ表が出る確率はnC2*{(1/2)^2}*{(1/2)^(n-2)}
・・・
9回だけ表が出る確率はnC9*{(1/2)^9}*{(1/2)^(n-9)}
となり、これらの確率を総和した確率は、コインをn回投げて、表が0~9回出る確率だ。余事象の考え方より、1からこの確率を引けば、表が10~n回出る確率が求められる。この計算を人の手で行うのは骨が折れるので、Excelに計算させた。その結果をグラフに示す。
グラフより、25回も投げれば約90%の確率で《偶然の出合い》に運勢カウンターが10個以上乗り、アップキープを待つばかりとなる。さらに、30回を超えると、コイントスを増やすことによる勝利条件達成への寄与がほとんど無くなる。つまり、30回投げようが40回投げようが1億回投げようが、ほぼ100%の確率で《偶然の出合い》に必要なだけの運勢カウンターを乗せることができる
逆に、ひりつくようなギャンブルのスリルを楽しみたいときは、20回程度のコイントスがお勧めだ。6~7割の勝率があるが、残りの3~4割は馬鹿にできない確率である。コンボを揃えておいて自分から不利な状況に突っ込むのはどうかと思うが、自分に課すハードルの高さを自由自在に調節することができるという点で、このコンボの可能性は無限大だ。
# 遠距離レス。お暇な方は検算してみてください。

コメント